4. Performance and Security Analysis

We provide detailed performance and security analysis in this section. All the tests presented in the sequel are run on an iMac with 3,2 GHz 8-Core Intel Xeon W with 32 GB 2666 MHz DDR4 RAM. The results are the averages of 100 runs.

4.1. Setup Related Tasks

In this section, we present the performance evaluation results for NP problem instance generation. The subgroup distance problem (SGD) relies on Max2SAT instances. We firstly create a Max2SAT instance using Motoki’s algorithm [Mot05]. Then, we convert the Max2SAT instance to SGD instance using our novel approach.

4.1.1. Max2SAT Instance Generation

For Max2SAT instance generation we use Motoki’s approach as presented in [Mot05] that proposes a randomized algorithm to generate test instances for the MAX 2SAT problem. The algorithm ensures that the generated instances have exactly one unsatisfied clause at the optimal solution, with a probability of 1. The author proves that the number of clauses in the generated instances is, with high probability, greater than the number of variables, aligning with known thresholds for unsatisfiability in random 2CNF formulas.

MAX 2SAT is a well-known NP-complete combinatorial optimization problem, where the goal is to find a truth assignment that maximizes the number of satisfied clauses in a 2CNF formula. To evaluate the performance of approximation algorithms for MAX 2SAT, both theoretical analysis and empirical studies are used. However, empirical studies require test instances with known optimal solutions. The paper addresses the challenge of generating such instances randomly.

The proposed algorithm generates an instance by first selecting a truth assignment t as the optimal solution. It then adds one randomly chosen clause that is unsatisfied by t and continues to add clauses satisfied by t until the formula becomes unsatisfiable. The algorithm ensures that the generated instance has a fixed optimal value, specifically one unsatisfied clause.

The paper analyzes the number of clauses added until the algorithm halts. It demonstrates that the threshold for the number of clauses is the number of variables, meaning that the algorithm is likely to stop only when the number of clauses exceeds the number of variables. This result coincides with the threshold for unsatisfiability in 2CNF formulas. The paper also provides a detailed mathematical analysis, proving that the algorithm works with high probability.

The paper presents a significant contribution to the generation of test instances for MAX 2SAT, providing a useful tool for evaluating approximation algorithms. The approach is mathematically rigorous and ensures that the generated instances meet the desired criteria with high probability.

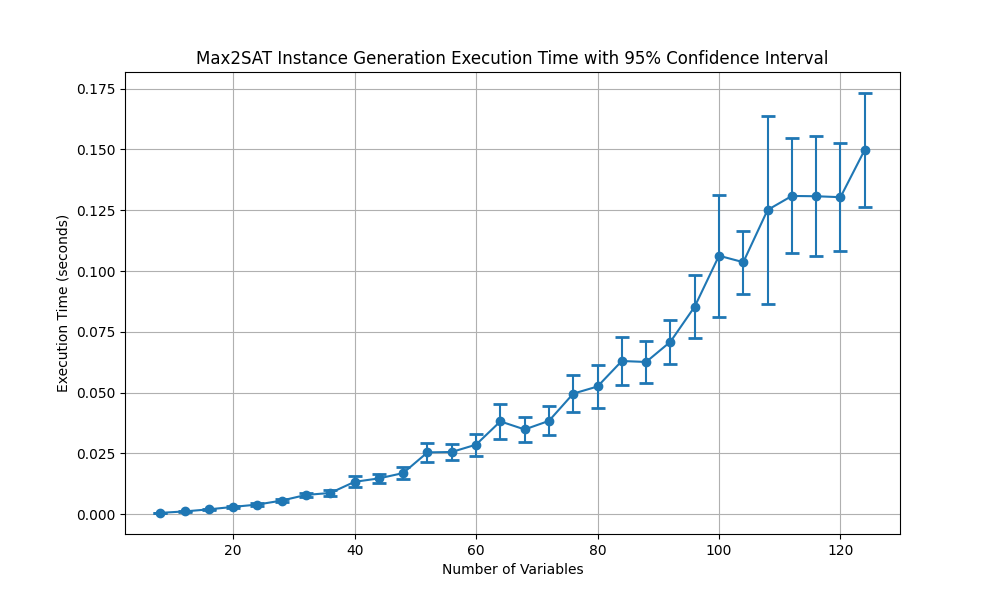
Fig. 4.1 The execution times with 95% confidence for Max2SAT problem instance generation.

Fig. 4.1 illustrates the execution time required to generate a Max2SAT instance as a function of the number of variables. The data points are plotted with error bars that represent the 95% confidence intervals, providing a visual indication of the variability in the measurements. As the number of variables increases, the execution time also increases. This is consistent with the expected behavior as more complex instances with larger numbers of variables require more computational resources to generate. The error bars show that the variability in execution time also increases with the number of variables, which is typical as the system may experience greater fluctuations in processing time due to the increased complexity of the problem instances. Overall, the figure effectively conveys the relationship between the number of variables in a Max2SAT instance and the time required to generate it, highlighting both the trend and the associated uncertainties.

4.1.2. Subgroup Distance Problem Generation

Fig. 4.2 illustrates the execution time required to generate an instance of the Subgroup Distance (SGD) problem as a function of the number of generators which is two times the number of variables in the employed Max2SAT instance. The plot includes error bars representing a 95% confidence interval, providing insight into the variability of the timing measurements. As the number of generators increases, the execution time rises significantly, showing a clear upward trend that appears to be nonlinear. This indicates that the complexity of generating an SGD instance grows rapidly with the number of generators. The increasing size of the confidence intervals for larger numbers of generators suggests that the variability in execution time also increases with the complexity of the problem. This could be due to factors such as increased computational demands and system resource allocation. Overall, the figure effectively conveys the relationship between the number of generators and the time required to generate an SGD instance, while also highlighting the increasing uncertainty in execution time as the problem size grows.

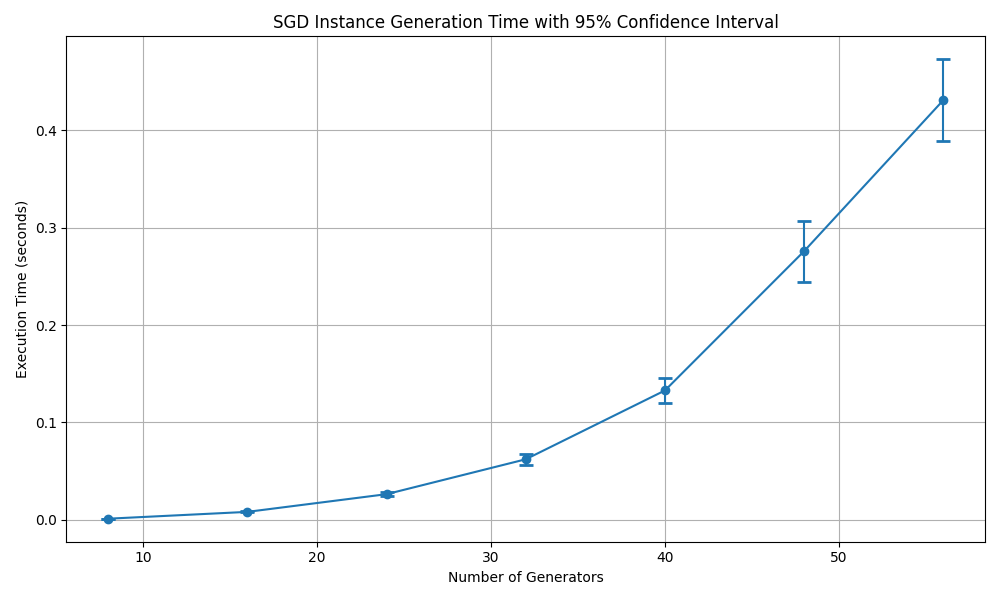
Fig. 4.2 The execution times with 95% confidence for SGD problem instance generation.

4.2. Prover Related Tasks

In SDZKP, the main computational load on the prover is the commitment generation. The response generation is O(1) since the computation effort for response generation is mainly handled during commitment generation. That is why, we present the commitment generation execution times here. Fig. 4.3 shows execution times for commitment generation by the prover as the number of generators in the SGD problem changes. The commitment generation algorithm linearly depends on the number of generators, therefore the execution time is a linear function of the number of generators. For an acceptable security level, for instance 128 bits of entropy, the commitment generation takes around 1 second.

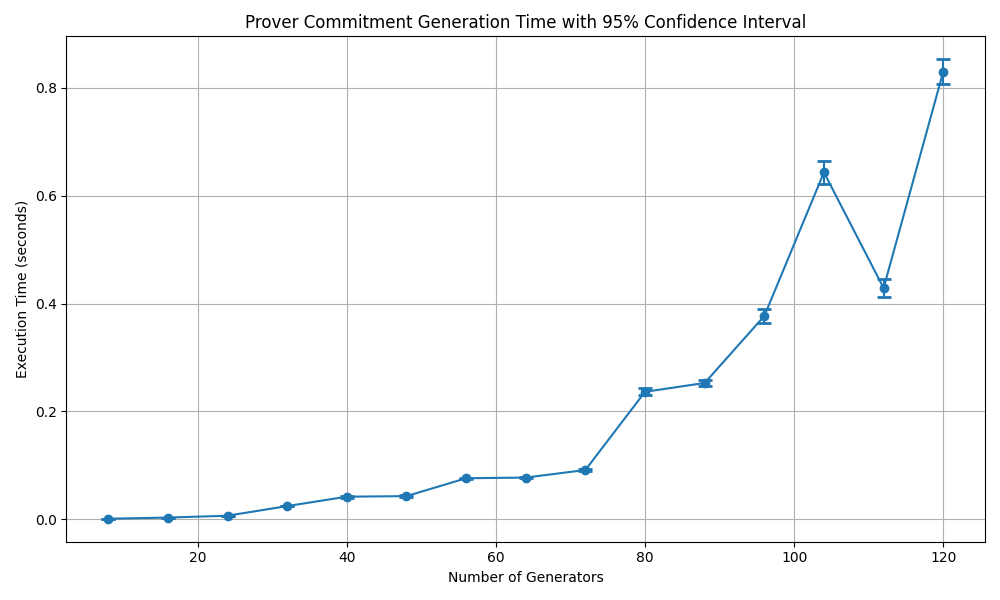
Fig. 4.3 The execution times with 95% confidence for commitment generation by the prover.

4.3. Verifier Related Tasks

Fig. 4.4 presents a line plot showing the relationship between the number of generators and the verification time by the verifier, including a 95% confidence interval. The x-axis represents the number of generators, ranging from around 10 to 120, while the y-axis measures the execution time in seconds, with values ranging from 0.00 to approximately 0.35 seconds. The plot reveals that the verification time remains relatively low and stable as the number of generators increases from 10 to around 90. The confidence intervals are visible as error bars, indicating greater variability in the verification time. In this experiment, we randomly select a challenge value from the set {0,1,2}. All the cases, contain code for honest prover; that is, the verification process has to provide True for all challenges. The spikes may be the result of discrepencies in random challenge selection process. All in all, the verification process takes almost a third of the commiment generation time. We can conclude that verifier’s computation load is considerably lower than that of the prover.

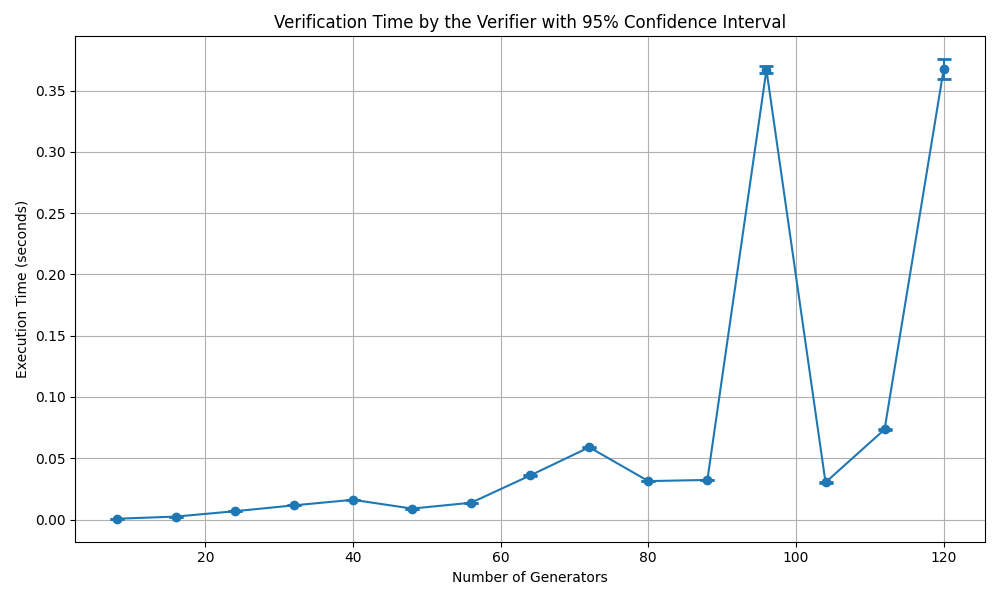
Fig. 4.4 The execution times with 95% confidence for commitment generation by the prover.

4.4. Security Related Validation

A zero-knowledge protocol has to satisfy completeness, soundness and zero-knowledge properties. In this section, we present the completeness and soundness validations for SDZKP. Please refer to [Onu24] for the theoretic proof for zero-knowledge property.

4.4.1. Completeness Validation

The benchmark code for validating the completeness of the SDZKP is designed to abort in any run if any round producess a verification failure (returns False). The code runs until completion proving that none of the rounds are False if the prover is honest and has the solution to the subgroup distance problem.

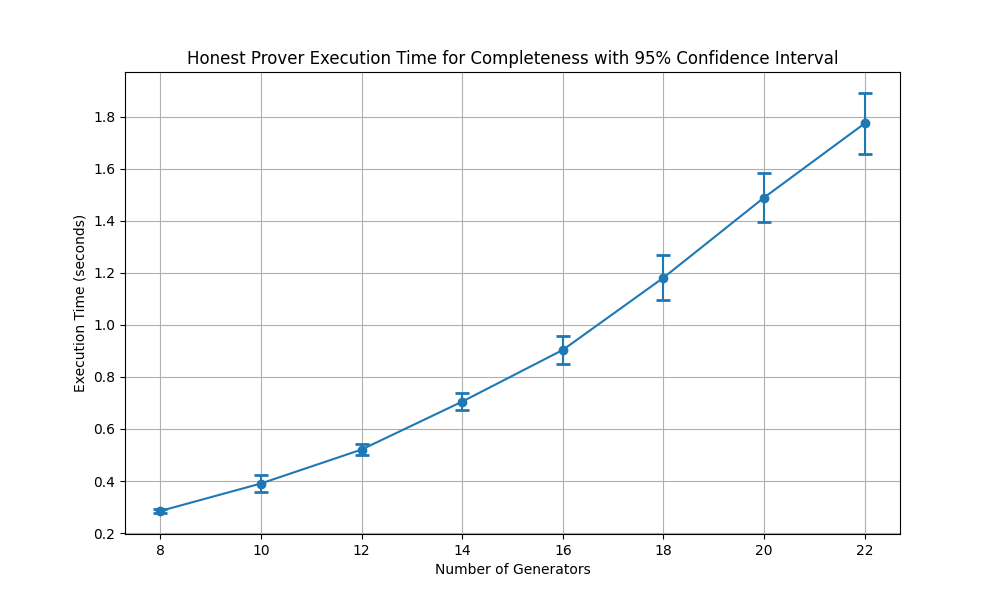
Fig. 4.5 The execution times with 95% confidence for completeness validation.

Fig. 4.5 depicts the execution time required for an honest prover to demonstrate completeness in a proof system, plotted against the number of generators. The plot shows a clear upward trend, indicating that as the number of generators increases, the execution time also increases significantly. The relationship between the number of generators and execution time appears to be approximately linear, as suggested by the straight-line pattern of the data points. The error bars, representing a 95% confidence interval, provide an indication of the variability in the measurements. The confidence intervals are relatively small, particularly for lower numbers of generators, suggesting consistent execution times in those cases. However, as the number of generators increases, the confidence intervals widen slightly, indicating a growing uncertainty or variability in execution time. This could be attributed to the increasing computational complexity as the problem scales.

4.4.2. Soundness Validation

In this scenario, the prover is dishonest, it knows the public parameters of the SGD problem. The dishonest prover creates a random solution; that is, it selects a subset of generators that produces a subgroup element randomly. Then, he tries to convince the verifier that it knows the solution. In any protocol run, if the verifier returns a False (not verified) result in any round, then the protocol run is assumed to fail, otherwise the protocol run is counted as verified. The benchmark code for validating the soundness of the SDZKP is designed to find the ratio of verified (returned True) protocol runs to the total number of protocol runs that we refer to as the cheating probability since the prover is dishonest. Fig. 4.6 shows the cheating probability for 1000 simulation runs where the number of generators is set to 8 in SGD problem. As expected, when the total number of rounds is 1 in a protocol run, then the cheating probability is \(\frac{2}{3}\). As the number of rounds increases, the cheating probability decreases exponentially with probability \((\frac{2}{3})^k\) where k is the total number of rounds in a protocol run. This trend is clearly visible in Fig. 4.6 . Approximately, after 16 rounds, the cheating probability becomes less then 0.001.

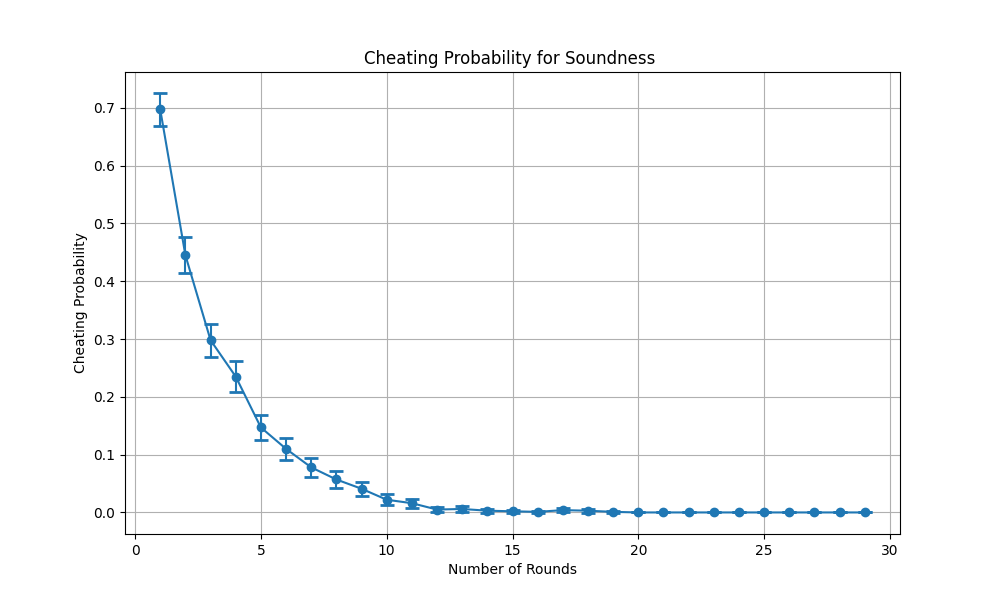
Fig. 4.6 The cheating probability for soundness validation.

Fig. 4.7 shows the execution times of the protocol run as the number of rounds in a run increases. As expected, a larger number of rounds in a run requires a larger amount of time to accomplish the verification process.

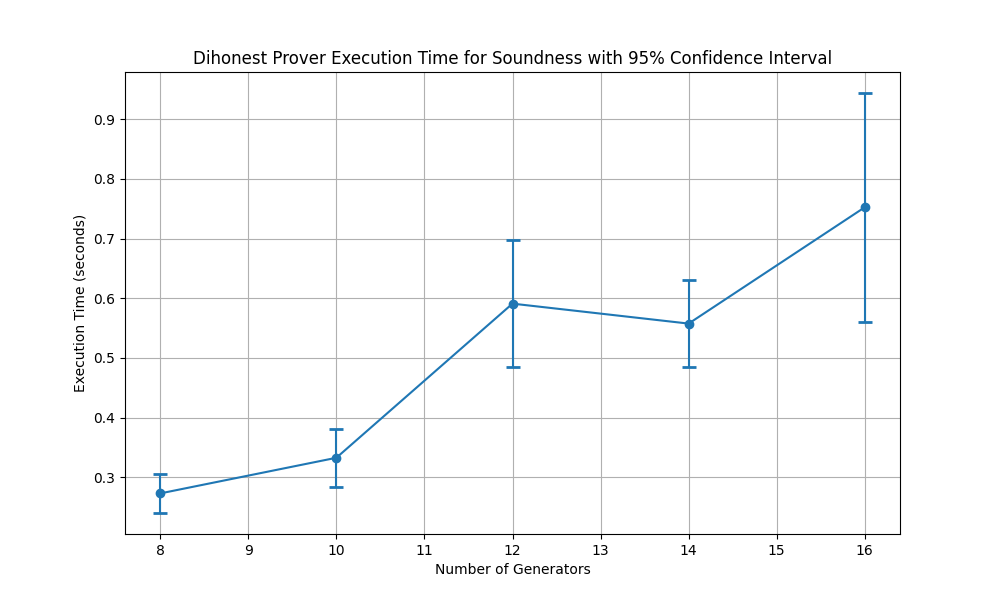
Fig. 4.7 The execution times with 95% confidence for soundness validation.