3. SDZKP Specification

In this section, we present the software design model of zero-knowledge proof (ZKP) schemes, the security requirements, performance metrics, adversary model and threat analysis. We highlight the fundamental principles of ZKP, distinguishing between proofs of membership and proofs of knowledge. We delve into the essential security properties of completeness, soundness, and zero-knowledge, outlining their formal definitions and practical implications.

3.1. Software Design Model

In a ZKP scheme, the statements (claims) are formally represented as a relation \(R\) between instances denoted as \(x\) and witnesses represented as \(w\). \(R\) defines the acceptable \((x,w)\) pairs; i.e., \(R\) consists of the pairs \((x,w)\). Then, the language \(L\) defines \(x\) that have an associated \(w \in R\); i.e., \(L=\{ x | \ (x,w)\in R \text{ for some } w \}\). Here, \(L\) is the set of instances induced by \(R.\) An instance is a commonly known input in an interactive proof scheme and a witness is a private information known by the prover. A membership claim can then be defined in the form of \(x \in L\) and a knowledge claim can be defined in the statement form of “Considering \(R\), I know the witness \(w\) associated with the instance \(x\).” In both types, the statements can be represented as software pieces or Boolean/Arithmetic circuits consisting of input nodes, output nodes and computation gates. The literature considers mostly the depth of the circuit \(d\), or circuit size \(C\) (i.e., the number of gates in the circuit) or the size of the input given to the circuit \(n=|x|\) where \(x \in L.\)

A zero-knowledge proof facilitates proving that a statement is true while preserving some secret (and privacy-sensitive) information. The claims about privacy-sensitive data can be defined as statements. For instance, the claim, “I am older than 18 years old” is a statement that is to be proven. An identity card (e.g., TCKK) is an instance of this statement. The birth date and personal information of the person signed by the government is the witness of this instance. A general claim (statement) is substantiated by the instance. The association between the instance and the secret information (or private information such as the actual age in this example) is called the witness. Claim (statement) and sometimes the instances are known to both of the principals (parties taking part in a protocol).

Zero knowledge proof schemes are seen in two types. A proof to assure that a statement is true or a proof of knowledge of an hidden information. The principals in a ZKP scheme are the prover (Alice or \(P\)) and the verifier (Bob or \(V\)) as shown in Fig. 3.1 that depicts the overall architecture of a ZKP scheme. In an abstract ZKP scheme as shown in Fig. 3.1 , the prover generates a proof of the statement and send it to the verifier. This step is called as the commit (\(a\), witness) phase. Subsequently, the verifier challenges the prover by posing some questions such as sending a binary sequence back to the prover; this phase is called as the challenge (\(c\)) phase. The prover prepares adequate response to the challenge and send it to the verifier (response, \(z\) phase). Finally the verifier accepts or rejects the claim without being able to reveal any confidential information.

A \(\Sigma\)-protocol shown in Fig. 3.1 is a three move (commit \(a\), challenge \(c\), response \(z\)) special honest verifier zero knowledge proof protocol which has special soundness [Dam02]. Security requirements completeness, soundness and zero-knowledge properties are given in Section 3.3 with their variants. A \(\Sigma\)-protocol can be converted to a non-interactive mode by employing the Fiat-Shamir transformation [FS86]. To employ this transformation, the prover runs the first step and produces the commitment \(a\). Then, instead of expecting a challenge from the verifier, the prover computes a (random) challenge by using a random oracle that accepts \(a\) and the statement circuit (\(x\)) as input. Using this challenge, the prover produces the response in step 3.

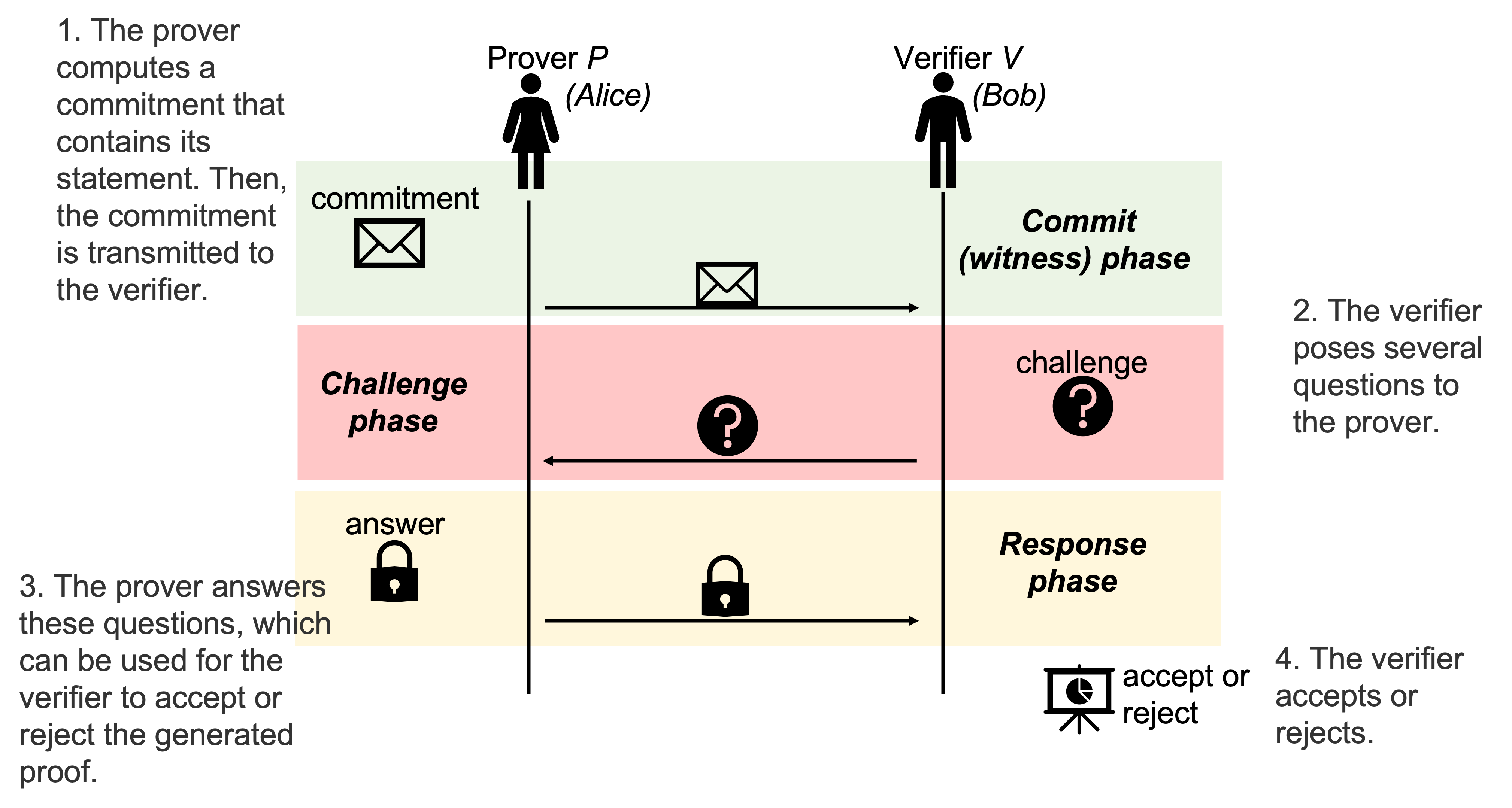
Fig. 3.1 The general architecture of a ZKP protocol.

Let us give a mathematical example initially presented by Tompa and Woll [Tom87] [TW87]. The set of integers between \(1\) and \(n\) that are relatively prime with \(n\) is denoted by \(Z_n^*.\) A number \(a \in Z_n^*\) is said to be a quadratic residue mod \(n\) if there exits \(x \in Z_n^*\) such that \(a=x^2.\) Say \(n=q_1q_2\) for distinct primes \(q_1\) and \(q_2.\) If the factorization of \(n\) is not known, then the problem whether \(a\) is a quadratic residue modulo \(n\) is known to be computationally hard. Alice wants to prove that she knows an element \(c \in Z_n^*\) such that \(a=c^2.\) Then, the steps of the ZKP scheme are:

Step 1 (commit phase): Alice (prover, \(P\)) chooses a random element \(k \in Z_n^*\) and computes \(K=k^2\) mod \(n.\) She sends \(K\) to Bob (verifier, \(V\)).

Step 2 (challenge phase): Bob chooses \(b \in \{0,1 \}\) uniform randomly and sends it to Alice.

Step 3 (response phase): Alice computes \(C=c^bk\) and sends it to Bob.

Step 4 (verification): Bob verifies \(C^2=a^bK\) mod \(n.\)

This protocol should be repeated sufficiently many times. If it is applied only once, Alice can cheat Bob with probability at most \(\frac{1}{2} .\) If it is repeated \(m\) times, then this probability is reduced to \(\frac{1}{2^m} .\)

SDZKP is a three move Stern-type zero-knowledge proof scheme similar to the architecture shown in Fig. 3.1. The details of the design decisions regarding the implementation of the protocol can be found in [Onu24].

3.2. Software Top-level Design

The SDZKP software system is a comprehensive Python implementation designed to facilitate a zero-knowledge proof (ZKP) protocol based on the subgroup distance problem within the Hamming metric. This software enables a secure, privacy-preserving communication mechanism between a Prover and a Verifier, which is essential in cryptographic applications where confidentiality and integrity are paramount. The system’s core functionality revolves around a 3-round ZKP protocol, where the Prover generates a proof based on the input parameters related to the subgroup distance problem, and the Verifier validates this proof without revealing any underlying information. This ensures that the process adheres to the principles of statistical zero-knowledge, meaning that no information about the Prover’s input (the witness) is leaked during the verification process. The soundness error of the protocol is deliberately set at 2/3, aligning with the theoretical underpinnings of zero-knowledge proofs in cryptographic research.

The architecture of the SDZKP system is divided into three primary modules: the Prover, the Verifier, and the gRPC Communication module. The Prover module is responsible for handling input parameters, generating the proof, and sending this proof to the Verifier via a secure gRPC interface. The Verifier module, on the other hand, receives the proof and performs a rigorous verification process to ensure the proof’s validity, again utilizing gRPC for secure communication. The gRPC Communication module plays a crucial role in maintaining the integrity and confidentiality of the data exchanged between the Prover and Verifier, ensuring that all transmissions are encrypted and secure.

In terms of non-functional requirements, the SDZKP system is designed with performance, scalability, and security in mind. The proof generation and verification processes are optimized for efficiency, minimizing latency in communication to ensure a smooth user experience. The system is also scalable, capable of handling larger instances of the subgroup distance problem without significant degradation in performance. Security is a fundamental aspect of the system, with rigorous measures in place to uphold the zero-knowledge property, ensuring that the process remains secure and that no unintended information is leaked.

The SDZKP project is built using Python, and all dependencies are managed via a requirements.txt file, ensuring easy setup and installation. The system is compatible with major operating systems that support Python, including Linux, macOS, and Windows. The project also includes comprehensive testing requirements, with unit tests developed for key functions within the Prover and Verifier components, as well as integration tests to ensure that the communication between these components is correctly implemented and secure. Additionally, security tests are performed to validate that the system adheres to the zero-knowledge principles.

Maintenance of the SDZKP system is facilitated through GitHub’s issue tracking feature, which allows for efficient management of bugs, feature requests, and other project-related tasks. Continuous integration and deployment (CI/CD) pipelines are also implemented, automating the testing and deployment processes to ensure that the system remains up-to-date and functional as new updates are made. Overall, the SDZKP software is a robust, secure, and scalable solution for implementing zero-knowledge proofs based on the subgroup distance problem, with a strong emphasis on performance, security, and ease of use.

3.3. Security Requirements

An interactive proof scheme (IP) is a two-party protocol between a prover and a verifier (turing machines) where the prover (P) has infinite computational power, while the verifier (V) operates within polynomial time. IP should satisfy two conditions, namely completeness and soundness. Completeness property means that if the statement is true, the prover can convince the verifier. Soundness property means, if the statement is false, a dishonest prover cannot mislead the verifier, except with negligable probability [GMR89] . An essential feature of interactive proofs is the randomness employed by the verifier. If verifier sends each random choices (coin tosses) it has done, then IP is called public-coin (or Arthur-Merlin game as introduced by Babai [Bab85]) Some IP protocols may require an initial trusted setup phase, potentially involving a trusted third party (TTP).

A zero-knowledge proof (ZKP) is an IP where the verifier learns nothing beyond the truth of the statement. If the prover convinces the verifier with just one message, the proof is non-interactive. Non-interactive ZKPs (NIZKP) can be achieved through a common reference string (CRS) or a random oracle model. A common approach to achive a NIZKP is to convert an interactive protocol into a non-interactive one using the Fiat–Shamir heuristic. The zero-knowledge property is shown by using a probabilistic polynomial-time algorithm called simulator. It ensures that the verifier gains no additional information by giving outputs indistinguishable from the verifier’s without having a witness. The idea of the simulation paradigm [Ode01] is “whatever a party can do by itself cannot be considered a gain from interaction with the outside.” Let us explain zero knowledge property more formally.

An IP \((P,V)\) is considered to have zero knowledge property if for every efficient (PPT) verifier \(V^*\), there exists an efficient simulator \(S_{V^*}\) such that for every true statement \(x,\) \(View_{V^*}[ P(x) \leftrightarrow V^*(x)]=S_{V^*}(x)\) where \(View_{V^*}[ P(x) \leftrightarrow V(x)]\) and \(S_{V^*}(x)\) denote all messages between \(P\) and \(V^*\) that appears in the real execution of the protocol (which is called the view of \(V^*\) on x) and output of \(S_{V^*}\) respectively. In the given scenario, the verifier might not adhere to the specified protocol and could attempt to cheat. If we limit the scenario to an honest verifier, the protocol is referred to as an honest verifier zero-knowledge proof.

In real life, the definition of zero knowledge proof schemes is often relaxed. This relaxation can be done in soundness or zero knowledge condition. For both conditions these relaxations give rise to three variants of the properties; namely, perfect, statistical and computational.

Perfect soundness is the original condition that a computationally unbounded cheating prover \(P^*\) can not convince \(V\). If this \(P^*\) has negligible probability of cheating the verifier, the protocol is said to have statistical soundness. It is said to have computational soundness if the probability of success of cheating prover \(P^*\) is negligable whenever \(P^*\) is probabilistic polynomial time. Zero-knowledge systems with computational soundness are also referred to as arguments, a term introduced by Brassard, Chaum, and Crepeau [BCCrepeau88].

Relaxation in zero knowledge property is done by allowing the simulator to sometimes fail. If we keep the original condition that the outputs of the actual protocol and the simulator are indistinguishable (i.e., absolutely no information is leaked) then we say the protocol has perfect zero knowledge property. statistical (a.k.a., almost-perfect) zero knowledge permits a negligible amount of information to leak, but this leakage is so minor that it remains insignificant, no matter how much computational power the verifier possesses. Although the two distributions differ, their statistical distance is negligible. If protocol allows for some information leakage, but only to an extent that is negligible for a verifier with limited (probabilistic polynomial-time) computational resources, then it is called computational zero knowledge.

Next we give a stronger property then soundness condition:

(Two) Special Soundness: A three round (commit, challenge, response) protocol for a relation \(R\) is said to have special soundness if there exists an efficient extractor \(A\) which computes a \(w\) satisfying \((x,w)\in R\) for any \(x\) and any pair of transcripts \((a,c,z),(a,c',z')\) with \(c\not=c'.\)

This definition is generalized as k-Special Soundness (see [ACK21]): A three round public-coin IP for relation \(R\) with challenge space consisting of \(N\) elements is said to be \(k\)-Special Sound (out of \(N\)) if there exists a PPT algorithm such that on input a statement \(x\) and \(k\)-many accepting transcripts \((a,c_1,z_1), \dots, (a,c_k,z_k)`\) for the same commitment with different challanges, it outputs a witness \(w`\) satisfying \((x,w) \in R.\)

It is known that a \(k-\) Special Sound IP with challenge space with \(N\) elements has knowledge soundness with knowledge error \(\frac{k-1}{N}\) [ACK21].

Special honest verifier zero knowledge property: A three round (commit, challenge, response) protocol for a relation \(R\) is said to have special honest verifier zero knowledge property if there exists an efficient simulator \(S\) which outputs an accepting transcript \((a,c,z)\) with distribution just like the real transcript for any given any \(x\) and \(c.\)

All in all, the ZKP implementations can be compared based on the following design choices [BBMT22]:

1. Types of supported statements: a ZKP of knowledge or a ZKP of membership.

2. Whether or not a trusted setup is required: When existing ZKP protocols are analyzed, the following possibilities for the trusted setup phase emerge:

   1. No setup: In this case, the ZKP scheme does not require any trusted setup phase; e.g., a copy of the security parameter is the only information required for initializing the ZKP scheme. For instance, bulletproof does not require any setup phase.

   2. Uniform random string (public coin): If the messages produced by the verifier are uniform random strings, and if those messages are independent of the prover’s messages, then we say that the setup phase employs public coins. All parties have access to an output of a uniform random number generator.

   3. Common reference string (CRS): When the setup phase employs a publicly known information called as CRS known to everybody. This is the generalization of the public coins. In CRS, the information does not have to be uniform random.

   4. Designated verifier setup: When the CSR is known only to a designated verifier, the setup phase is called as designated verifier setup. In this approach, the setup algorithm executed by the prover is correlated with the setup algorithm executed by the verifier; and this requires a trust to the setup phase.

   5. Random oracle model: The setup phase defines a common cryptographically secure hash function that acts as a random oracle to produce nonces (numbers used once and never repeated) that are never used in the past invocations of the algorithm.

3. Interactive or not.

4. Assumptions about the underlying intractable problem: Most of the works in the literature using group theoretic approach allocates DLP.

3.4. ZKP Performance Metrics

The efficiency of ZKP implementations can be compared based on the following performance metrics [BBMT22]. Here, we list the most-commonly used metrics.

1. Proof size (succinctness): the size of the proof in comparison to the circuit size (\(C\)) representing the statement.

   1. Fully succinct: \(\mathcal{O}(1)\)

   2. Polylog succinct: e.g., \(\mathcal{O}(\log^2 C)\)

   3. Sqare root succinct: \(\mathcal{O}(\sqrt{C})\)

   4. Depth-succinct: e.g., \(\mathcal{O}(d \log C)\) assuming that the depth of the verification circuit is \(d.\)

   5. Non-succinct: the proof is not sublinear in \(C\).

2. The time complexity for the trusted setup (if exists)

3. The time complexity of the tasks executed by the prover \(P:\) efficiency of the proof generation

4. The time complexity of the tasks executed by the verifier \(V\): efficiency of the proof verification

In addition to these metrics, round complexity, parallelizability, batching, memory consumption, number of operations in the algorithms, memory consumption, disk and storage requirements can be considered as additional performance metrics for comparing various ZKP proposals [BBMT22].

Zero-Knowledge Succinct Non-Interactive ARgument of Knowledge (zk-SNARK) is a non-interactive ZKP protocol initially proposed by Bitansky et al. in 2011. They showed that if there exist extractable collision-resistant hash functions (ECRHs) and an appropriate private information retrieval scheme, then there exist SNARKs for NP. Also in this work, they propose candidates for ECRH constructions. One of these is based on the hardness of discrete logarithm problem and the two others are based on hard problems on lattices namely, knapsack (subset-sum) problems. In 2016, Groth constructed an efficient zk-SNARK for Quadratic Arithmetic Programs where he used bilinear groups. Zcash uses Groth’s construction. A downside of zk-SNARK is it uses non-public randomness in its setup phase. In other words, zk-SNARK requires a trusted setup. Also, it is not quantum-safe. A remedy to these problem is zk-STARK.

Scalable Transparent Zero-knowledge Argument of Knowledge (zk-STARK) introduced by Ben-Sasson et al. in 2018. It is an Interactive Oracle Proofs (IOP) system. zk-STARK is more transparent, i.e., it needs no trusted set-up. zk-STARKS rely on collision-resistant hash functions. The zk-STARK-friendly hash function [BSGL20] [CBD+20] is the focus of extensive research campaign. Relying on hash functions, it is quantum resistant. A major disadvantage of zk-STARKS is the proof size compared to zk-SNARKS. There are some recent works that try to reduce the proof length.

Zk-SNARK’s algorithmic complexity for prover \(\mathcal{O}(C\log(C))\) and verifier \(\mathcal{O}(1)\) are lower compared to zk-STARK’s complexity that is \(\mathcal{O}(C \text{polylog}(C))\) and \(\mathcal{O}(\text{polylog}(C))\), respectively. The proof size of zk-SNARK is \(\mathcal{O}(1)\) whereas it is \(\mathcal{O}(\text{polylog}(C))\) for zk-STARK.

Aurora [BSCR+19] is a Zk-SNARK proposed by Ben-Sasson et al. in 2019. They developed the protocol for Rank-1 Constraint Satisfaction (R1CS) which is an NP-complete language. Aurora employs a public (transparent) setup phase. It is lightweight and quantum-safe. For the same number of constraints defined in R1CS, they accomplished reducing the proof size to 20 times shorter than the previous Zk-SNARK proposals. Aurora uses an interactive oracle proof for solving univariate version of the sumcheck problem [LFKN92].

Hyrax [WTS+18] is another Zk-SNARK variant proposed by Wahby et al. in 2017. They convert an interactive proof of arithmetic circuit (AC) satisfiability to a ZKP scheme. Hyrax’s proofs are sublinear in circuit size (succinct), does not require a trusted setup phase, secure under the discrete log assumption.

Ligero is a zero knowledge argument based on a chosen collision-resistant hash function. By making it non-interactive in the random oracle model, an efficient zk-SNARKs can be obtained that do not require a trusted setup or public-key encryption.

Bulletproof is a short zero-knowledge proof depending on the hardness of discrete logarithm problem and has no trusted setup. It uses Pedersen vector commitment and has very short the proof size by groundbreaking method inner product algorithm. It can be non-interactive using Fiat-Shamir heuristic. One disadvantage of Bulletproof is, it takes more time to verify a bulletproof than to verify a SNARK proof.

Libra [XZZ+19] is zero-knowledge proof scheme that has both optimal prover time with a succinct proof size and \(\mathcal{O}(d \log C)\) verification time. Different from the other proposals, Libra employs a one-time setup phase that does not have to be repeated per statement. It relies on the GKR protocol [GKR15].

3.5. Adversary Model and Threat Analysis

An adversary is a (malicious) attacker carrying out an attack on the protocol and an adversary model is the formal definition of the attacker in a security protocol. Depending on the level of formalization, it may be a set of statements about the capabilities (skill sets, advantages, assumptions, and also limitations) of the attacker and its goal. An adversary model can be an algorithm having some computation power. Adversary models are generally used to prove the security of the protocol. A widely used model is the Dolev-Yao model [DY83]. In the Dolev–Yao model, the adversary can listen to communication between the principals and can send data/messages to principals. It may act as a man in the middle.

An adversary model usually defines

1. the assumptions about the attacker

   1. assumptions about the environment: whether the adversary is an insider or outsider. Connectivity of the adversary to the protocol infrastructure can also be evaluated here.

   2. intellectual resources: the intellectual resources of the adversary based on competence and knowledgeability.

   3. capabilities: the privileges of the adversary and whether or not it is active

   4. computational resources; e.g., number of CPUs, memory, etc.

   5. amount of accessible data

2. the goal(s) of the adversary.

While designing a zero knowledge protocol, the main security concerns are whether or not completeness, soundness and zero knowledge properties are satisfied. However, when zero-knowledge proofs are employed in applications such as identification or authentication, additional attacks can be implemented by an adversary. Below we briefly define the attack vectors and the associated adversary models are presented in Table 3.1 [MBA20] [WEAK+19] [GKR+21] [PPP+21] [DNS04] [UWL21].

1. Impersonation attacks (masquerading as prover)

2. Mutual impersonation: person-in-the-middle attack

3. Replay attacks

   1. General replay attacks (resending previously captured messages)

   2. Interleaving attack (a selective combination of information from previous protocol executions is used to attack the protocol)

   3. Reflection attack (some messages are replayed back to the sender)

   4. Delay attack (some messages are delayed by an active adversary)

4. Integrity attack (some messages are intelligently modified by an active adversary)

5. Brute force attack (all possible combinations to solve the intractable problem are tried)

6. Quantum attack (whether or not the protocol is quantum-safe?)

7. Redundancy information attack (a passive adversary listens to all messages on the channel and tries to derive useful information)

8. Timing attack (a passive adversary has access to system clocks and can measure how much time it takes for algorithms to run.) [DNS04]

Table 3.1 Potential attacks and the adversary model.

Attack	Goal(s)	Location	P/A	Resources	A ccessible data
Im personate as prover	Break s oundness, cheat verifier	Insider outsider	Active	Bounded	Some :mat h:(x,w) pairs
Mutual impe rsonation (person in the middle)	Break com pleteness and soundness	Insider outsider	Active	Bounded	Public data
Replay attacks (inte rleaving, re flection, delay)		Insider outsider	Active	Bounded	Public data
Integrity attack	Modify messages to break soundness	Insider	Active	Bounded	Public data and p reviously captured messages
Brtute force attack	Break zero- knowledge	Outsider	P assive	Bounded Unbounded	Public data
Quantum attacks	Break zero- knowledge	Outsider	P assive	Quantum computer	Messages on channel
R edundancy in formation attack	Break zero- knowledge by eave sdropping messages or by analyzing public data	Outsider	P assive	Unbounded	Messages on channel
Timing attacks	Reveal secret in formation	Insider	P assive	Bounded	System clocks